Week 12 FAQs
📚 Topics Covered in Week 12
- Loss Functions for Classification
- Neural Networks
- Architecture
- Parameters
- Activation Functions
- Forward Pass
🔍 Loss Functions for Classification
The misclassification error, also known as the 0-1 loss, is defined as:
\[ \min \frac{1}{n} \mathbb{I} [h(\mathbf x_i) \neq y_i] \]
Graphical Representation:
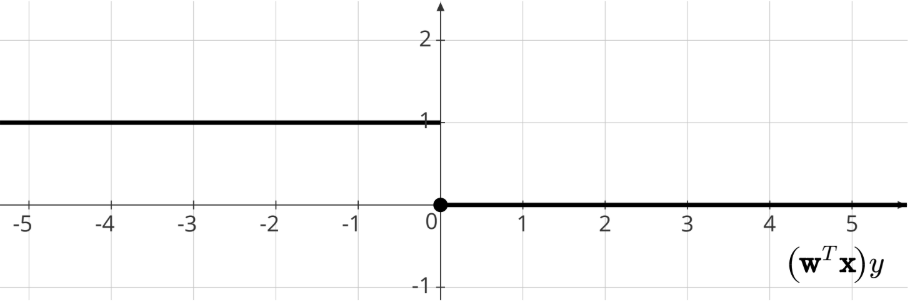
This is an NP-hard problem. To address its complexity, alternative loss functions are employed. These functions approximate the behavior of the 0-1 loss while offering better optimization properties, particularly convexity. Here are some common alternatives:
1. Squared Loss
\[ [(\mathbf w ^T \mathbf x)y - 1]^2 \]
Graphical Representation:
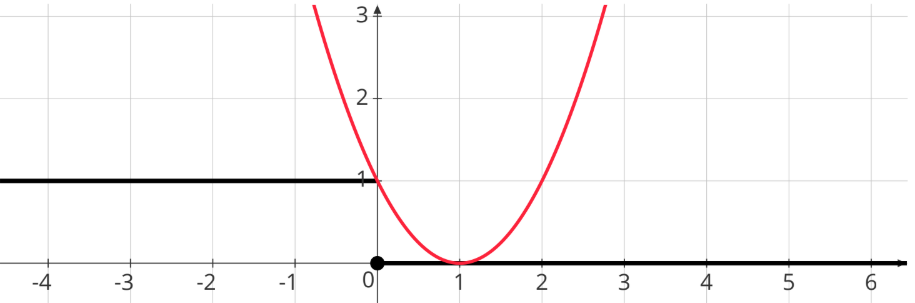
2. Hinge Loss
\[ \max (0, 1 - (\mathbf w^T \mathbf x)y) \]
Graphical Representation:
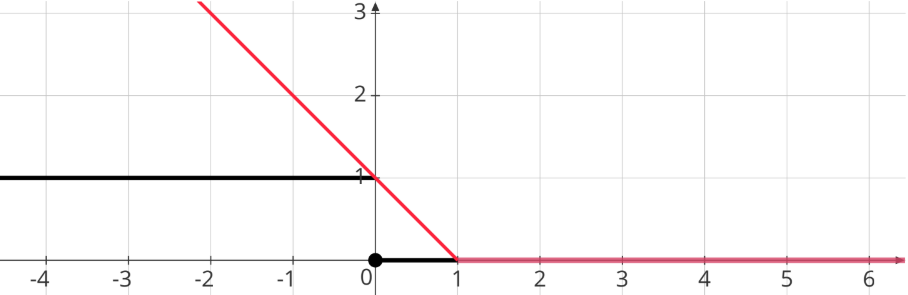
3. Logistic Loss
\[ \ln (1 + e^{- (\mathbf w ^T \mathbf x)y}) \]
Graphical Representation:
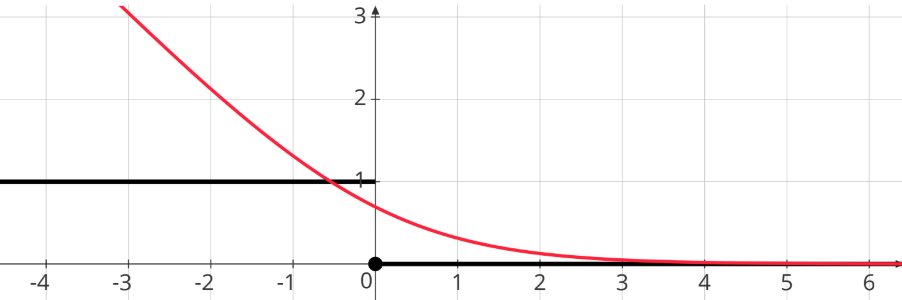
4. Perceptron Loss
\[ \max (0, - (\mathbf w^T \mathbf x)y) \]
Graphical Representation:
🔍 Neural Networks
🧩 Architecture
A neural network typically consists of the following layers:
- Input Layer
- Hidden Layers
- Output Layer
Each neuron in the network is connected to every neuron in the succeeding layer.
⚙️ Parameters
Each neuron (except those in the input layer) has associated weights and a bias term.
Total Parameters Calculation:
- Weights:
\[ \sum_{i=1}^{n-1} (\text{neurons in layer}_i \times \text{neurons in layer}_{i+1}) \]
Where \(n\) is the total number of layers, and each term in the sum represents the number of connections between layer \(i\) and layer \(i+1\).
Biases:
Sum of neurons in all layers except the input layer.
Example:

In this example:
- Input Layer: 3 neurons
- Hidden Layer: 4 neurons
- Output Layer: 2 neurons
Calculations:
Weights:
\[ (3 \times 4) + (4 \times 2) = 20 \]Biases:
\[ 4 + 2 = 6 \]Total Parameters:
\[ 20 + 6 = 26 \]
⚡ Activation Functions
- ReLU (Rectified Linear Unit)
\[ g(x) = \max(0, x) = \begin{cases} x & \text{if } x \geq 0 \\ 0 & \text{if } x < 0 \end{cases} \]
Graphical Representation:
- Sigmoid Function
\[ g(x) = \frac{1}{1 + e^{-x}} \]
Graphical Representation:
🔄 Forward Pass
For a detailed explanation of the forward pass and related computations, refer to this session: 📺 Watch here
💡 Need Assistance?
Feel free to reach out for any queries: 📧 22f3001839@ds.study.iitm.ac.in